What Is An Ionic Solid

Backdrop of Solids

As you should call up from the kinetic molecular theory, the molecules in solids are non moving in the same manner equally those in liquids or gases. Solid molecules just vibrate and rotate in place rather than movement nearly. Solids are generally held together by ionic or potent covalent bonding, and the attractive forces betwixt the atoms, ions, or molecules in solids are very stiff. In fact, these forces are and so strong that particles in a solid are held in stock-still positions and have very little freedom of movement. Solids have definite shapes and definite volumes and are not compressible to whatsoever extent.

There are 2 main categories of solids—crystalline solids and amorphous solids. Crystalline solids are those in which the atoms, ions, or molecules that make up the solid be in a regular, well-defined arrangement. The smallest repeating blueprint of crystalline solids is known every bit the unit jail cell, and unit of measurement cells are like bricks in a wall—they are all identical and repeating. The other main type of solids are called the amorphous solids. Amorphous solids do not have much order in their structures. Though their molecules are close together and accept little freedom to move, they are not arranged in a regular guild as are those in crystalline solids. Common examples of this type of solid are drinking glass and plastics.

There are four types of crystalline solids:

Ionic solids—Fabricated up of positive and negative ions and held together by electrostatic attractions. They're characterized by very high melting points and brittleness and are poor conductors in the solid land. An example of an ionic solid is tabular array salt, NaCl.

Molecular solids—Made upwardly of atoms or molecules held together by London dispersion forces, dipole-dipole forces, or hydrogen bonds. Characterized by low melting points and flexibility and are poor conductors. An example of a molecular solid is sucrose.

Covalent-network (also called atomic) solids—Made up of atoms connected by covalent bonds; the intermolecular forces are covalent bonds likewise. Characterized equally being very hard with very high melting points and being poor conductors. Examples of this type of solid are diamond and graphite, and the fullerenes. As you tin see below, graphite has merely 2-D hexagonal structure and therefore is not difficult like diamond. The sheets of graphite are held together past only weak London forces!

solid1

Metallic solids—Made up of metal atoms that are held together by metallic bonds. Characterized by loftier melting points, can range from soft and malleable to very hard, and are good conductors of electricity.

CRYSTAL STRUCTURES WITH CUBIC UNIT CELLS (From https://eee.uci.edu/programs/gchem/RDGcrystalstruct.pdf)

Crystalline solids are a three dimensional drove of private atoms, ions, or whole molecules organized in repeating patterns. These atoms, ions, or molecules are called lattice points and are typically visualized as round spheres. The ii dimensional layers of a solid are created past packing the lattice point "spheres" into square or airtight packed arrays. (See Beneath).

Packing Arrays
Effigy 1: 2 possible arrangements for identical atoms in a 2-D structure

Stacking the two dimensional layers on meridian of each other creates a three dimensional lattice point organisation represented past a unit cell. A unit jail cell is the smallest collectionof lattice points that tin be repeated to create the crystalline solid. The solid tin can be envisioned as the result of the stacking a great number of unit cells together. The unit cell of a solid is adamant by the type of layer (square or close packed), the style each successive layer is placed on the layer below, and the coordination number for each lattice point (the number of "spheres" touching the "sphere" of interest.)

Primitive (Simple) Cubic Structure

Placing a second square array layer directly over a first foursquare array layer forms a "simple cubic" structure. The simple "cube" advent of the resulting unit cell (Effigy 3a) is the basis for the proper name of this three dimensional structure. This packing arrangement is often symbolized equally "AA...", the letters refer to the repeating order of the layers, starting with the bottom layer. The coordination number of each lattice point is six. This becomes apparent when inspecting part of an adjacent unit cell (Figure 3b). The unit cell in Figure 3a appears to contain 8 corner spheres, withal, the total number of spheres within the unit of measurement cell is 1 (only 1/8th of each sphere is really inside the unit of measurement cell). The remaining seven/8ths of each corner sphere resides in 7 adjacent unit cells.

Simple Cubic

The considerable space shown betwixt the spheres in Figures 3b is misleading: lattice points in solids touch as shown in Effigy 3c. For example, the distance between the centers of two side by side metal atoms is equal to the sum of their radii. Refer once again to Figure 3b and imagine the next atoms are touching. The edge of the unit of measurement jail cell is then equal to 2r (where r = radius of the atom or ion) and the value of the face diagonal as a function of r can be institute by applying Pythagorean'south theorem (a² + b² = c²) to the correct triangle created by two edges and a face diagonal (Figure 4a). Reapplication of the theorem to some other right triangle created past an border, a face diagonal, and the body diagonal allows for the determination of the torso diagonal as a function of r (Figure 4b).

Edges

Few metals adopt the elementary cubic construction because of inefficient use of space. The density of a crystalline solid is related to its "percent packing efficiency". The packing efficiency of a unproblematic cubic construction is only virtually 52%. (48% is empty infinite!)

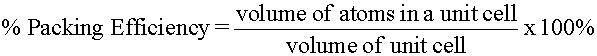
Packing Efficiency

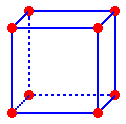
Body Centered Cubic (bcc) Construction

A more efficiently packed cubic structure is the "body-centered cubic" (bcc). The starting time layer of a square assortment is expanded slightly in all directions. Then, the second layer is shifted so its spheres nestle in the spaces of the first layer (Figures 5a, b). This repeating order of the layers is often symbolized every bit "ABA...". Like Effigy 3b, the considerable space shown between the spheres in Effigy 5b is misleading: spheres are closely packed in bcc solids and touch on along the torso diagonal. The packing efficiency of the bcc structure is about 68%. The coordination number for an cantlet in the bcc structure is viii. How many full atoms are in that location in the unit prison cell for a bcc construction? Describe a diagonal line connecting the three atoms marked with an "x" in Figure 5b. Assuming the atoms marked "ten" are the same size, tightly packed and touching, what is the value of this torso diagonal as a function of r, the radius? Find the border and volume of the cell every bit a part of r.

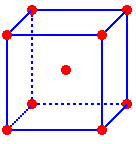
Body Centered Cubic

Cubic Closest Packed (ccp)

A cubic closest packed (ccp) structure is created past layering close packed arrays. The spheres of the second layer nestle in half of the spaces of the first layer. The spheres of the third layer directly overlay the other half of the start layer spaces while nestling in half the spaces of the second layer. The repeating order of the layers is "ABC..." (Figures six & vii). The coordination number of an cantlet in the ccp structure is twelve (vi nearest neighbors plus three atoms in layers above and below) and the packing efficiency is 74%.

Figure 6: Close packed Assortment Layering. The 1st and 3rd layers are represented past lite
spheres; the 2d layer, dark spheres. The 2nd layer spheres nestle in the spaces of the 1st
layer marked with an "ten". The third layer spheres nestle in the spaces of the 2nd layer that
direct overlay the spaces marked with a "·" in the 1st layer.

Figure 7a & 7b: 2 views of the Cubic Close Packed Structure

If the cubic shut packed structure is rotated past 45° the face centered cube (fcc) unit of measurement cell can be viewed (Figure 8). The fcc unit prison cell contains 8 corner atoms and an atom in each face. The face atoms are shared with an adjacent unit cell so each unit of measurement cell contains ½ a face atom. Atoms of the face centered cubic (fcc) unit cell bear upon across the face diagonal (Figure 9). What is the edge, face diagonal, body diagonal, and book of a face centered cubic unit cell as a function of the radius?

Figure 8: The face centered cubic unit cell is drawn by cut a diagonal airplane through
an ABCA packing arrangement of the ccp structure. The unit cell has 4 atoms (1/eight of
each corner atom and ½ of each face cantlet).

Figure 9a:Space filling model of fcc. Effigy 9b: The face of fcc. Face diagonal = 4r.

Ionic Solids

In ionic compounds, the larger ions become the lattice point "spheres" that are the framework of the unit of measurement prison cell. The smaller ions nestle into the depressions (the "holes") betwixt the larger ions. There are three types of holes: "cubic", "octahedral", and "tetrahedral". Cubic and octahedral holes occur in square array structures; tetrahedral and octahedral holes announced in shut-packed array structures (Figure 10). Which is unremarkably the larger ion – the cation or the anion? How tin the periodic table be used to predict ion size? What is the coordination number of an ion in a tetrahedral pigsty? an octahedral hole? a cubic hole?

Figure ten. Holes in ionic crystals are more like "dimples" or "depressions" between the
closely packed ions. Small ions tin can fit into these holes and are surrounded by larger ions
of opposite charge.

The blazon of hole formed in an ionic solid largely depends on the ratio of the smaller ion's radius the larger ion's radius (r_smaller/r_larger). (Tabular array 1).

Table 1

Empirical Formula of an Ionic Solid

Two ways to decide the empirical formula of an ionic solid are: ane) from the number of each ion contained within one unit of measurement cell ii) from the ratio of the coordination numbers of the cations and anions in the solid.

Table 2

Instance: Notice the empirical formula for the ionic compound shown in Figures eleven & 12.First Method: When using the first method, retrieve virtually atoms in a unit of measurement cell are shared with other cells. Table 2 lists types of atoms and the fraction contained in the unit jail cell. The number of each ion in the unit cell is determined: ane/8 of each of the 8 corner X ions and i/4 of each of the 12 edge Y ions are constitute within a single unit cell. Therefore, the cell contains 1 X ion (eight/8 = ane) for every three Y ions (12/4 = 3) giving an empirical formula of XY3. Which is the cation? anion? When writing the formula of ionic solids, which comes first?

Second Method: The second method is less reliable and requires the exam of the crystal construction to determine the number of cations surrounding an anion and vice versa. The structure must be expanded to include more unit cells. Figure 12 shows the same solid in Figure 11 expanded to four next unit cells. Examination of the structure shows that there are 2 X ions coordinated to every Y ion and 6 Y ions surrounding every X ion. (An boosted unit of measurement cell must exist projected in front of the page to see the sixth Y ion ). A 2 to half-dozen ratio gives the aforementioned empirical formula, XY3.